Sidebets and Fair Cake-Cutting

I went up to Genesis this weekend, the biggest and longest-running Smash Bros tournament. I hadn’t been to a major tournament in 7 years (since my first kid popped), and it was great to reconnect with the smash scene again. Made a deep run in bracket, played in a crew battle, ran into old friends, and met new ones in-person for the first time. It’s reassuring to know that, no matter where I move or how I grow, I can always make friends and find a home in the Melee community. The actual spectator experience was a drag – this Genesis must’ve been the most boring grand finals in the last decade. But the upside was that I made $140 in side bets.

I’ve got a system for conducting side bets. Here’s how it works:

• The proposer sets the odds; e.g. “KC Chiefs 2 : 1 Philly Eagles”

• Anybody can accept the offer on either side; e.g. “$20 on Chiefs”

• The proposer takes the other side of unmatched bets ; e.g. match with $10 on the Eagles

I swear this is great game design and better than how most people conduct side-bets. Let me explain.

Normie Bet Flaws

Most people propose bets in a particular format. The proposer picks a side and offers the other. E.g. “I like the Chiefs! Anyone want the Eagles?” The odds are assumed to be 1:1. This is simple and understandable, but it has some critical design flaws that cause bets to go unmatched.

Firstly, the bet is one-sided. The proposer is explicitly picking a side (Chiefs), and asking for someone to take the other side. Most social groups are pulling for the same side, so if somebody wants to bet on the Chiefs, it’s likely that most of their friends also want to bet on the Chiefs. Nobody wants to be the contrarian buzzkill rooting for the other side.

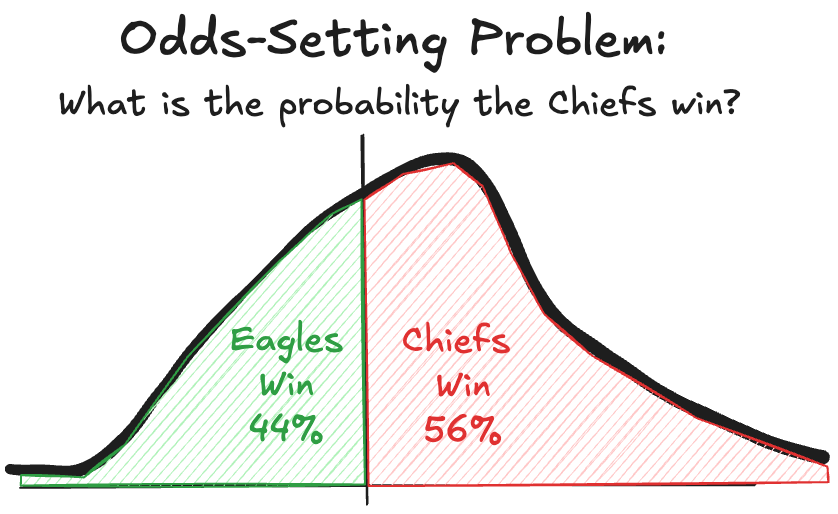
Secondly, the bet is imbalanced. 1:1 bets are simpler to explain and execute, but they are rigidly locked to even odds. Most outcomes do not have a 50% probability. As a result, the 1:1 bet is often skewed towards one side (in the superbowl’s case, 56 Chiefs : 44 Eagles). This means that taking the Eagles’ side of the Chiefs 1 : 1 Eagles bet is a negative expected value, and an obviously poor decision. Even if somebody wanted to play, their odds are likely bad.

As a result of these two issues, the basic one-sided 1:1 bets often go unmatched. If bet proposals go unmatched, the proposers get shy and stop offering, and the action stops.

Market Liquidity to the Rescue

My system addresses both of these issues. With a two-sided bet, fans of either side have an opportunity to take the offer. With flexible odds, the payouts can shift to balance the expected values on both sides. As a result, bets are far more likely to be taken. Players always have the opportunity to bet on their favorite team or find a positive expected value wager.

The odds setter is at a theoretical disadvantage here. If I set Chiefs v Eagles at 60:40, but the actual odds are 56:44, then a savvy bettor could profit at my loss by taking the undervalued Eagles. To compensate for this risk, professional bookies take a % cut from either side, profiting from any bet that takes place. In a casual friendly betting environment, this feels distasteful. Instead, my house rule is that the winningest player ought to set the odds. This creates a rubber-banding effect where the player who is ahead is at a disadvantage, and offers losers a comeback opportunity.

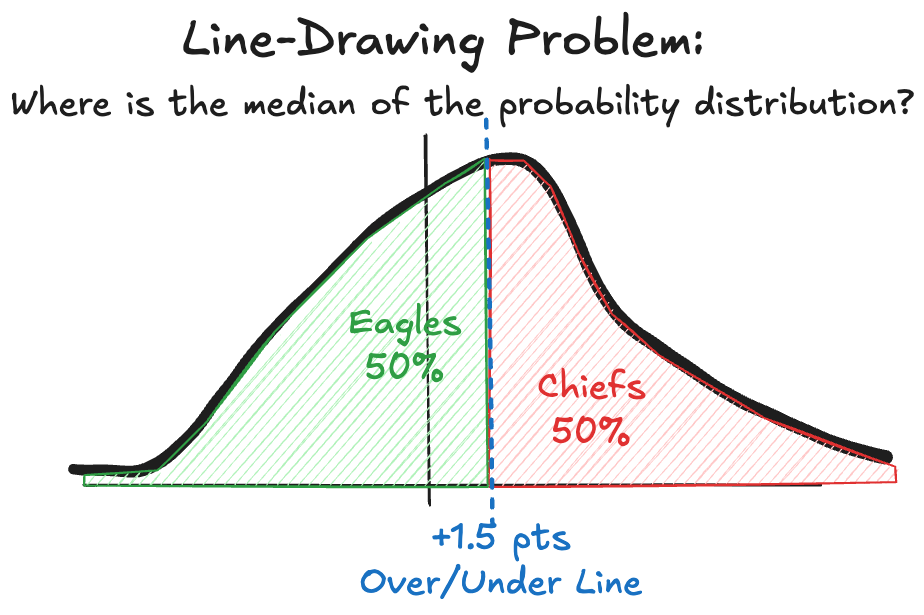
An alternative to odds-setting is to draw an over-under line. Instead of saying Chiefs 56 : 44 Eagles, you might say Chiefs win by 1.5pts over/under. This means that if you believe the Chiefs will win by 2pts or more, you bet “over”, and vice-versa. The payout odds for over-unders are always 1:1, which simplifies the math.

In finance jargon, the line-drawing bookie is a market maker who provides liquidity to ensure that trades can happen. Since market-making is risky, the market-maker usually takes a % cut in the form of a bid-ask spread. However, the greater this cut, the less incentivized players are to bet on either side. If liquidity is low, trades (bets) can’t take place, and there is no action to be had. My system is specifically designed to generate greater liquidity.

Fair Cake-Cutting

Despite the disadvantage of the odds setter, I find it to be a compelling intellectual exercise. Effectively, I need to accurately gauge the probability that an event occurs and set the odds accordingly. For example, if I believe that the Chiefs have a 66% likelihood to win, I would set the odds at 2:1. If I deviate too far from reality, then I stand to lose a lot. This probability evaluation exercise forces me to block out my cognitive biases and try to evaluate the situation as objectively as possible.

This exercise in odds setting is known in economic game theory as the “fair cake-cutting problem”. In a nutshell, one player has to cut a cake into slices, and everybody else gets to pick their slices before the cutter. As a result, the cutter wants to cut the cake as evenly as possible, to maximize the value of the worst possible slice.

For over/under line-drawing, the exercise is in determining the median of a probability distribution. For odds-setting, the exercise is in determining what fraction of the probability distribution lies above or below 0.

Magic the Gathering players are likely familiar with this exercise, as there’s been a dozen cards with similar effects. Fair cake-cutting with qualitatively different resources offers a unique challenge, especially when the value of different resources varies by game state.