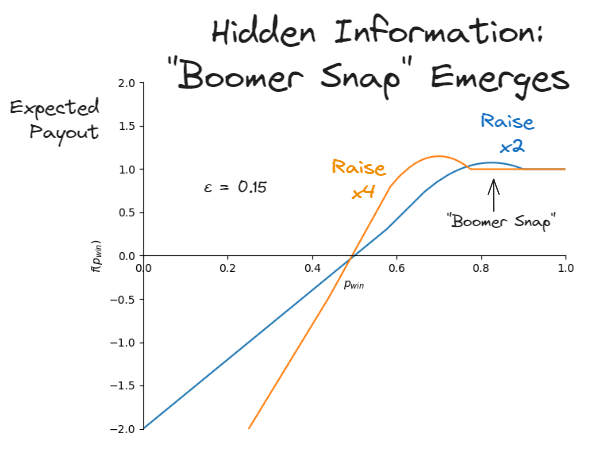
“Boomer Snap” is a meme in the Marvel Snap community, wherein a player with a dominant position raises on the final turn. Boomer snaps are seen as mistakes commonly made by inexperienced players, and there is plenty of advice online to NEVER BOOMER SNAP.
But what is actually wrong with boomer snaps? Why don’t we see similar advice in poker and backgammon? In this article, I’ll delve into a simple betting model that shows the game theory behind the mistake, and when it may actually be correct to boomer snap.
First, some context. Marvel Snap employs poker-like betting mechanics. Players enter a match wagering 1 point and can “Snap!” on any turn to double their wager. Their opponent is given the option to either match the raise, or to retreat and forfeit the pot. Additionally, the game will always double the wager on the final turn. If you snap on this final turn, you are effectively re-raising to quadruple your wager. This is the notorious “boomer snap”.
For clarity’s sake, I will use poker terminology throughout the article:
Poker | Marvel Snap | Description
Check | No Snap | no action taken
Raise | Snap! | double the wager
Call | Accept Snap | accept the doubled wager
Fold | Retreat | forfeit and give up the pot
We will work through two simple models and find that, with perfect information, there is no “boomer snap” – if you are in the lead, it is always correct to raise more. However, when we introduce hidden information (e.g. cards in hand, judgment error), then it is better to raise less when in a dominant position.
Perfect Information Model
Suppose both players can see their opponents’ cards and are perfect probability computers. They still do not see the results of any future randomness, like dice rolls or card draws. This is a “perfect information” game, analogous to backgammon, or playing poker with players’ hands revealed.
Our simple perfect information game works as follows:
There are two players, A and B.
The game is zero-sum, so B’s payout is the negative of A’s payout
The stake is initially set to 1
Both players know the probability of A winning, P(win)
The decision tree is as follows:
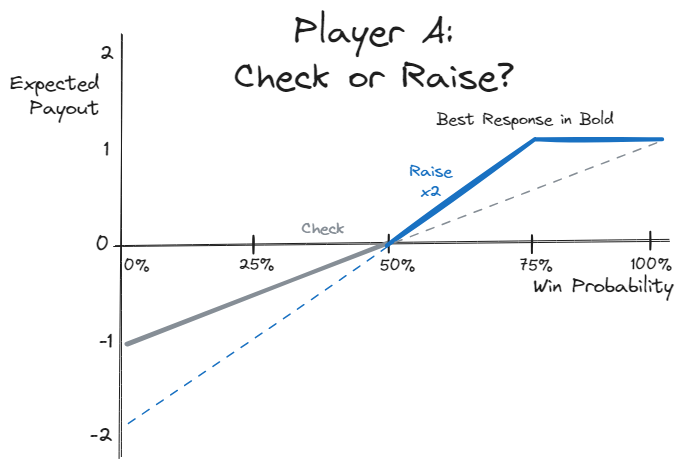
Player A can choose to check or raise
If check, the game resolves. A receives payout = 2 * P(win) - 1
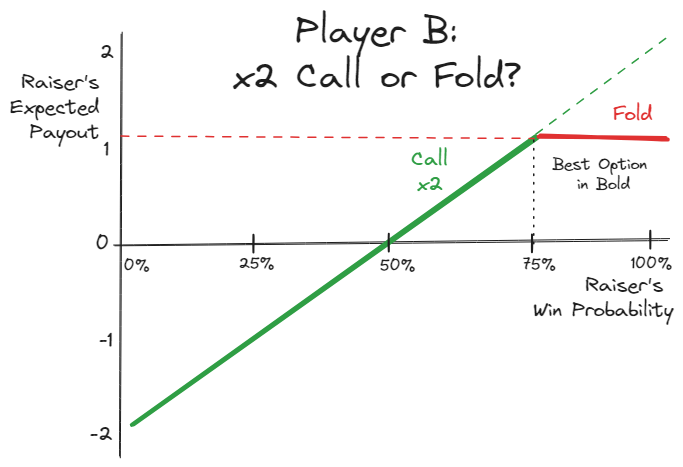
If raise, Player B can choose to fold or call
If fold, A receives payout = 1
If call, A receives payout = 4 * P(win) - 2
Solving this backwards:
B will fold instead of call if their payout is higher.
That is, if -1 > -4 * P(win) + 2
⇒ B will fold if P(win) > 75%
*Note, P(win) is player A’s chance of winning.
A’s payout for raising is:
If P(win) > 75%, payout = 1
If P(win) < 75%, payout = 4 * P(win) - 2
A will raise instead of check if their payout is higher
⇒ A will raise if P(win) > 50%
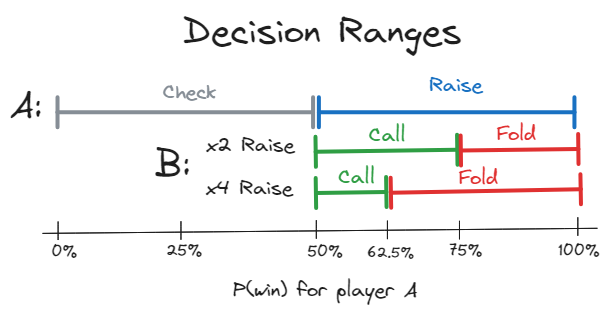
If we alter this slightly so that the raise factor is x4 instead of x2, then we get similar results:
A will raise if P(win) > 50%
B will fold if P(win) > 62.5%
These results are intuitive to anyone who has played poker. You should raise if you are winning. Opponents are more likely to fold if the raise is larger.
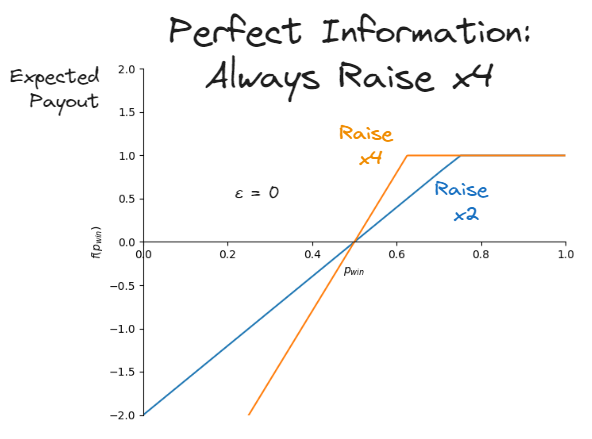
In our perfect information game, boomer snaps seem like a good idea. The x4 raise payout is greater or equal to than the x2 payout if you are in the lead. The x4 raise seems particularly good if you are in a dominant position, as you are even more confident that you are in the lead. We need something more to explain boomer snaps.
Hidden Information
Of course, Marvel Snap is not a perfect information game. Opponents cannot see the cards in your hand. Additionally, players are not perfect computers. They might misjudge the situation and miscalculate P(win), which can be interpreted as hidden information. Given the variety of cards and decks, Snap seems to have even more hidden information than Poker. Let’s add this to our model.
In our hidden information game, there is one change:
Both players know the probability of A winning, P(win)Both players perceive p̂(win), a noisy signal for P(win)
p̂(win) is in the range [P-ε, P+ε], uniformly distributed
ε is the error term. Larger values of ε represent more hidden information
Note that p̂(win) is unbiased. The expected value of p̂(win) is the true value P(win). Payouts are still calculated based on P(win)
Players’ decisions are based on the expected value of payouts, conditional on p̂(win).
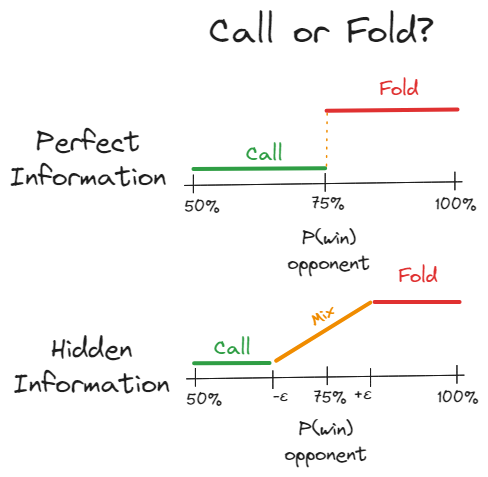
A will raise instead of check if p̂(win) > 50%
B will fold instead of call if p̂(win) > 75%
The proof is left as an exercise to the reader.
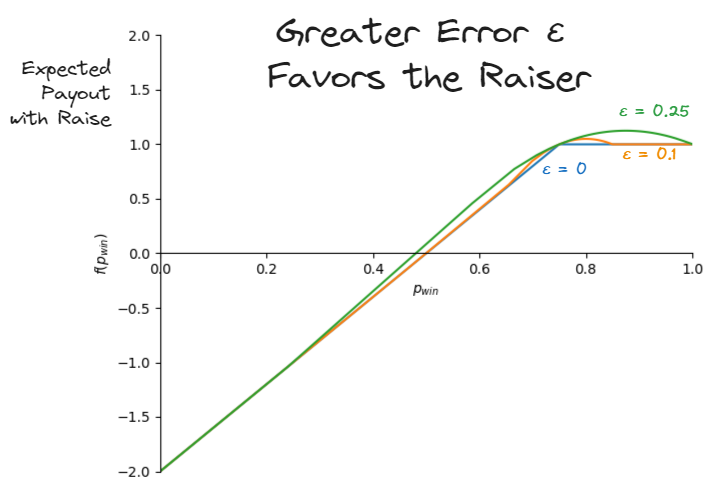
The randomness introduced by ε adds error to the decision-making. For example, consider B’s decision to fold when P(win) = 73%. In the full information game, B should certainly call. However, in the hidden information scenario, B might perceive p̂(win) = 77% and choose to fold instead of call. There is a range of 75% +/- ε where the decision is probabilistic. The more hidden information, the larger this error range.
This change in decision-making also changes the payouts. Since B makes mistakes choosing to call or fold, A gets larger payouts from raising in the range around the indifference point P(win) = 75%. The larger the error ε, the larger the range.
Now let us consider different raise amounts. Both the x2 and x4 raises gain a payout boost from decision-making error around the indifference point. However, the call-or-fold indifference points are not the same – x2 raise’s point is at 75%, and x4 raise’s point is at 62.5%. There is a range where the x2 raise is actually better than the x4 raise, since your opponent may mistakenly call the x2 raise but fold against the x4 raise.
This explains the infamous Boomer Snap! When your P(win) is very high, you should not raise too much. Better to give your opponent the rope to hang themselves. This again mirrors conventional wisdom from poker, where you should try to lure your opponent in rath Notably, this also suggests there is a correct time to boomer snap – if your P(win) is close to 62.5%, you have a lot of potential to gain from a x4 raise, as it will encourage opponents to fold decent hands.
Assumptions, Extensions, and Caveats
There are several other factors that affect boomer snaps that I assumed away. Extending our model to include this would likely further bolster the case against boomer snaps.
Betting signals. We assumed players’ beliefs about P(win) were not changed by their opponent’s decisions. In reality, if my opponent bets, I should suspect that their hand is stronger than anticipated. In stats terms, this is a Bayesian update to p̂(win), and improves the decision-making on whether to call or fold. For Marvel Snap in particular, the final turn’s automatic raise does not offer a signal to the opponent, since you did not opt into it. Boomer snaps signal a particularly strong hand, while quietly accepting the final turn’s raise may allow your strong position to fly under the radar.
Asymmetric information. We assumed that both players had the same error ε. However, if your opponent has more information than you, then that further muddies the decision. This scenario often arises in Marvel Snap, as one player may have played more cards to create a winning board state, but the other player may have more cards in hand or have been preparing a powerful combo for the final turn.
Raise error. We ignored the effect of hidden information on player A’s decision to check or raise. If p̂(win) is only slightly above 50%, then it’s possible player A may be raising with a losing hand. This makes raising more dangerous, especially in the range where boomer snaps are theoretically optimal, p̂(win) = 62.5%.
Multiple turns. My game was a single turn affair, but betting in Snap and Poker occurs over multiple turns. In Snap, you can only “snap!” once in the whole game. A boomer snapper held onto their one snap until the final turn. If they have a dominant lead, they likely should have snapped earlier. This is similar to poker, where strong hands will push repeated small raises rather than a single aggressive raise.
Curiosity calls. Players in both poker and snap like to see the final outcome and will often make bad bets just to see the result. This may be for a sense of excitement, closure, or information about their opponent’s bluffing habits. Empirically, new Snap players bias strongly towards playing it out, and skilled players are more willing to take strategic retreats. In an extended affair like a poker tournament or conquest mode in Snap, it may be valuable to pay for information on your opponent’s playstyle.
Verdict: Are the Boomers Wrong?
Boomer snaps are a phenomenon created by hidden information. The more hidden information, the worse boomer snaps are. In this context, “hidden information” includes cards in hand, betting signals, and errors in judgment. However, there is certainly still a time and place to perform a boomer snap. Counter-intuitively, boomer snaps are ideal when you have a slight lead but not a dominant one.